When it comes to standardized testing, there’s nothing more frustrating for students than losing points on questions they know how to answer. In Algebra, one of the most common places for careless errors is on questions requiring the distributive property. Let’s take a look at a couple reasons why.
Negative Signs
Students must use the distributive property when they need to get rid of parentheses. Students should first recognize that when they are asked to simplify an expression that has parentheses and none of the answer choices have parentheses, this is a clue that they’ll need to use this method.
With the distributive property, you distribute the coefficient outside of the terms in parentheses among each of the individual elements inside the parentheses.
However, students are often not cautious about keeping track of the negative signs.
–4(x – 4) = (–4)(x) – (–4)(4)
(–4)(x) – (–4)(4) = –4x – (–16)
–4x – (–16) = –4x + 16
The questions writers expect this and often lay trap answers for the solutions based on missed negative signs. The best away around this trap is for students to show their work throughout the entire process of solving these problems. The test is designed to take advantage of students who use mental math when it comes to distribution. When students try to rush and skip steps, they increase their chance of making a careless error. Teach students to avoid these traps on the test by showing their work.
Try this problem with students.
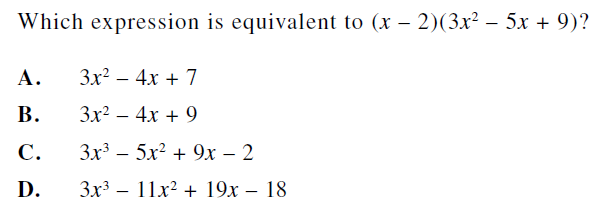
(x – 2)(3x2 – 5x + 9)
First, distribute the x to each term in the second polynomial.
Then distribute the –2 to every term in the second polynomial.
3x3 – 5x2 + 9x – 6x2 + 10x – 18
Combine like terms.
3x3 – 5x2 – 6x2 + 9x + 10x – 18
3x3 – 11x2 + 19x – 18
By working one step at a time, students can avoid the mistakes that cause inaccuracies on their exam.
Exponents
Another one of the most common ways the test causes students to miss out on points is by testing rules for distributing exponents in complex distribution problems.
The most important rules to know for the test are how to multiply exponents of the same base and how to calculate a term with an exponent raised to another exponent. Review these rules with your students before exam day:
- When multiplying terms with exponents that share a common base, add the exponents.
(25)(23) = 2(5 + 3) = 28
Possible trap answers:
x15 (multiplying the exponents)
x2 (subtracting the exponents)
(x4)(x6) = x(4 + 6) = x10
Possible trap answers:
x24 (multiplying the exponents)
x–2 (subtracting the exponents)
- When an expression with exponents is inside parentheses and there is an exponent outside the parentheses, the exponents are multiplied together.
(42)3 = 4(2 · 3) = 46
Possible trap answers:
x5 (adding the exponents)
x–1 (subtracting the exponents)
(a6)2 = a(6 · 2) = a12
Possible trap answers:
x8 (adding the exponents)
x4 (subtracting the exponents)
If students struggle to remember which rule is which, teach them to write out the exponents in full to solve problems.
(x4)(x6) = = x(4 + 6) = x10
(x4) = x · x · x · x
(x6) = x · x · x · x · x · x
(x4)(x6) = x · x · x · x · x · x · x · x · x · x = x10
(a6)2 = a(6 · 2) = a12
(a6) = a · a · a · a · a · a
(a6)2 = (a · a · a · a · a · a)(a · a · a · a · a · a) = a12
Exponent Shortcut: When calculating an exponent times an exponent, remember that times starts with t, and use a plus sign (the shape of a t).
Let’s take a look at an example:
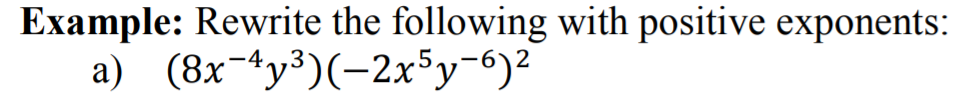
(8x–4y3)(–2x5y–6)2
(8x–4y3)[(–2)2(x5)2(y–6)2]
(8x–4y3)(4)(x5 · 2)(y–6 · 2)
(8x–4y3)(4x10y–12)
(8 · 4)(x–4 · x10)(y3 · y–12)
32(x–4 + 10)(y3 + –12)
32(x6)(y–9) or 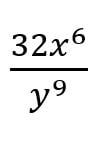
Students who show their work and carefully work through negative signs and exponents are far less likely to make careless errors in questions testing the distributive property. Teaching students these methods empowers them to work through the test with confidence, earning the points they deserve.
What careless errors do your students make in Algebra, and how do you help them?